Enunciado

Un perrito esta atado a dos postes A y B separados una distancia unitaria con dos correas. Cada correa tiene longitud uno. Un pajarito esta atado a dos puntos C y D separados una distancia unitaria con dos piolines. Cada piolin tiene longitud uno.

• a. ¿Sobre que superficie puede moverse el perrito?
• b. ¿Sobre que volumen puede moverse el pajarito?

Superficie en la que puede moverse el perro

Este problema del Coding Contest se me hizo puramente matemático y con matemática simple, cálculos de áreas, volumen e intersecciones básicamente. No se hizo necesario un script, pero genere algo pequeño para probar con diferentes radios. El problema podría ser mas interesante si los radios y las distancias no fueran la misma. Vamos a la solución que propuse.

El perro si estuviera atado a un solo punto puede moverse dentro de un circulo, al estar atado a dos puntos, se puede mover solamente en la interseccion de los dos circulos.

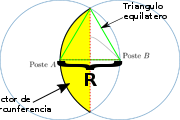
En la intersección de los dos círculos, se pueden distinguir dos segmentos de círculos, la suma de estas dos áreas es el área buscada. A su vez, los centros de cada uno de los círculos con cada uno de los puntos de intersección forman dos triángulos equilateros de lado R(Radio=1), la suma de las alturas de estos triángulos es la longitud de la cuerda de los segmentos.

El área de un segmento de circulo es: $\frac{R^{2}}{2}(\Omega - \sin( \Omega ))$ , $\Omega$ es el angulo el arco de circunferencia para el segmento, en este caso es $120º=\frac{2}{3}\Pi$ por los dos triángulos equilateros(los ángulos internos son 60º) antes mencionados. Entonces: $Area = R^{2}( \frac{2}{3}\Pi - \sin{ ( \frac{2}{3}\Pi ) })=R^{2}( \frac{2}{3}\Pi - \frac{\sqrt 3}{2})$ Para el caso de $ R=1 $ el área resulta $Area = 1,228370$

Volumen en el que puede moverse el pajarito

El caso es análogo al anterior, solo que resulta de la intersección de dos esferas, que son en las que se podría mover si solo estuviera atado de un punto

En este caso la porción de volumen que se puede mover en casa esfera es el volumen correspondiente a un casquete de altura $ h = R \over 2 $ . La altura(h) del casquete se puede ver en base al problema anterior, pensando los circulos como una vista en corte de las esferas.

El Volumen de un casquete es: $ \frac{1}{3} \pi h^{2}(3R-h) $ Para el caso es dos veces este volumen, resultando: $ vol = \frac{1}{6}\pi R^{2}(3R-\frac{R}{2})=\frac{5}{12}\pi R^{3} $

Resultando: $ Volumen = 1,308997 $

Nota: No es necesario un script, ya que estan expuestas las formulas necesarias y se puede realizar facilmente con una calculadora, de todos modos se planteo un pequeño script, para generar rapidamente soluciones para otros valores de R. El script esta realizado en python(2.7), y hace uso del modulo math. Se invoca de la siguiente manera:

$ python solucion.py R

donde R es el radio, en este caso:

$ python solucion.py 1