El Primo De Fibonacci

El primer problema del CITES Coding Contest trataba sobre la sucesion de Fibonacci y los numeros primos:

Enunciado

Considere la sucesión de Fibonacci cuyo n -ésimo elemento f(n) está definido como

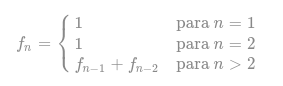
• a. ¿Para qué valores de n ≤ 90 se da que f(n) es primo?
• b. ¿Cuántas cifras tiene el valor f(1477) escrito en base diez?

Solución

Lo primero a atacar fue como generar la sucesión de Fibonacci o mejor aun dado un n devolver el elemento f(n) correspondiente según la sucesión. No iba a generar toda la sucesión completa hasta el n dado, seria un desperdicio.

La primer opción fue usar la la formula explicita pero por trabajar con numero irracional, para números altos(n mayores a 80) en mi caso devuelve resultados erróneos.

Finalmente utilice un algoritmo presente en la wikipedia que implementado en Python resulta:

El paso siguiente era determinar si el numero en cuestión era o no primo, hay mucha teoría sobre los números primos, y existen varios test de primalidad, acá decidí utilizar el test de Miller-Rabin, la implementación del mismo la tome desde un topic en stackoverflow

Nota: El test se corre con k=7, esto determina la confiabilidad del test, a mayor k menor es el error. Se puede reducir el k a fin de optimizar tiempos, pero se reduce la confiabilidad del test. El próximo punto del problema era determinar los decimales de un dado n, acá recurrí a la opción mas fácil lo transformo en un string y determino la longitud del mismo. El script completo es el siguiente(esto se encuentra en el repositorio del Coding Contest):

Se le pasa como argumento el n que se desea evaluar y devuelve todos los n tales que f(n) sea primo, y la cantidad de cifras para f(n) Por ejemplo para los puntos pedidos:

$ python primo_fibonacci.py 90
Los numeros primos para n <= 90 son:  [3, 4, 5, 7, 11, 13, 17, 23, 29, 43, 47, 83]
El numero fn(90) tiene 19 cifras

$ python primo_fibonacci.py 1477
Los numeros primos para n <= 1477 son:  [3, 4, 5, 7, 11, 13, 17, 23, 29, 43, 47, 83, 131, 137, 359, 431, 433, 449, 509, 569, 571]
El numero fn(1477) tiene 309 cifras

En la solución que envié al concurso, leí mal y en vez de devolver los n primos devolvía los f(n) por lo que seguramente fue computado como solución incorrecta.